미적분 7번째 개념입니다.문제집에서는 도함수 활용 2에서 나오는 단원입니다.이 단원에서는 변곡점의 개념과 곡선의 오목함과 볼록함, 다양한 함수 그래프 그리기, 방정식과 부등식 활용, 속도와 가속도에 대해 배웁니다.개념 정리는 강한 수학을 참고했습니다.이 자료는 선행용이 아니라 복습용 자료입니다.

원래 파일입니다. 첨부파일U20210523_235611339_미적7.pdf 파일 다운로드 내 컴퓨터 저장

네이버 MYBOX에 저장
지난 단원에서는 함수의 증가와 감소, 최대와 극소에 대해 배웠습니다.복습하러 간다! 도함수 활용 1이기 때문에 이번 단원에서는 본격적으로 변곡점을 찾아 그래프를 그려보도록 하겠습니다.예전에는 단순히 f'(x)가 0이 되는 값을 이용해 극값 정도만 찾아줬더니 변곡점 개념이 들어가 다양한 함수도 그릴 수 있게 됐습니다.조금 복잡할 수도 있지만 너무 재밌기 때문에

잘 따라와 주세요.

곡선의 오목과 볼록, 변곡점
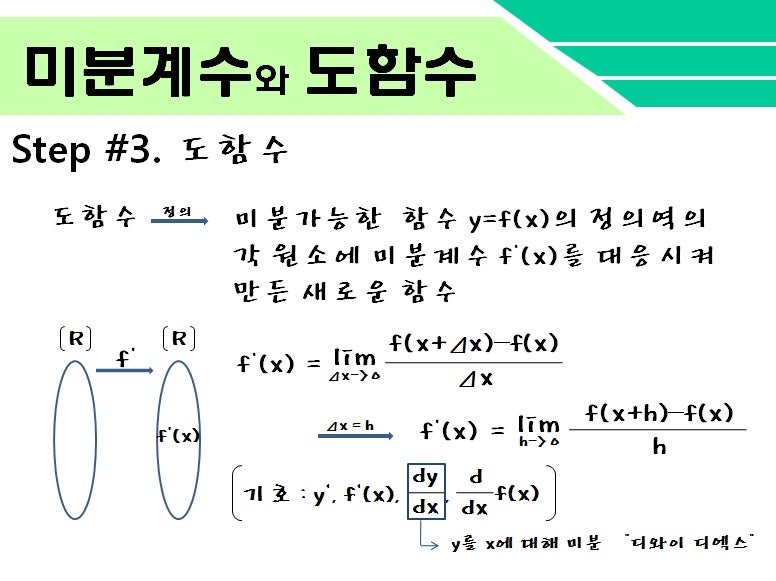
과거 개념 정리에서 일부 가져온 이미지입니다.오목과 볼록이 갈라지는 경계가 되는 점이 변곡점입니다.위에 그림을 보시면 f(x)와 f'(x), f'(x)를 같이 그려서 변곡점을 기준으로 f'(x)의 부호와 f'(x)의 부호를 알 수 있습니다.f'(x)>0 → f'(x)의 기울기 > 0 → f(x) 아래에 볼록f'(x)<0 → f'(x)의 기울기 <0 → f(x)위에 볼록을 잘 기억해 두세요.
함수 그래프

함수 그래프
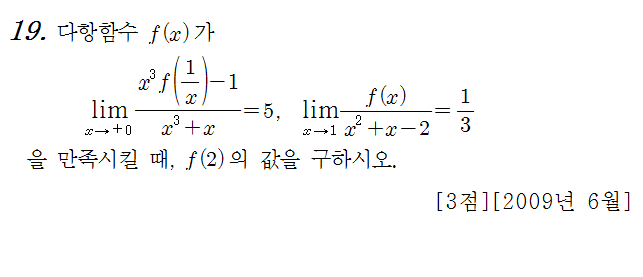
그림 하나 그려보면서 설명해볼게요. $f\left(x\right)=\frac{x}{x^2+1}$f(x)=xx2+1

f'(x)와 f'(x)를 구하고 증감표를 구하세요.도함수와 이계도함수는 분의 미분법을 이용하여 구하면 됩니다.기억 안 나면 복습하고 올게.様々な微分法を復習する $f”\left(x\right)=\frac{-x^2+1}{\left(x^2+1\right)^2}$f′(x)=-x2+1(x2+1)2$f”\left(x\right)=\frac{2x\left(x^2-3\right)}{\left(x^2+1\right)^3}$f′′(x)=2x(x2−3)(x2+1)3

극치는 +1과 -1이고 변곡점은 √3과 0, -√3으로 잡죠 증감표를 그려볼게요.

구체적인 그래프의 형태를 알려고 f'(x)와 f'(x)도 함께 표에 넣었습니다.통상 최대치의 최소치를 구하는 문제는 변곡점까지 취할 필요는 없습니다.빨간 색 화살표를 그린 것이 보이시나요?f'(x)<0에서 f'(x)<0이라고, 아래로 내려가면서 위에 볼록니 처음의 붉은 화살표 형태가 나옵니다.f'(x)<0에서 f'(x)>0이라고, 아래로 내려가며 밑으로 볼록이므로 2번째 빨간 화살표의 모양이 나옵니다.f'(x)까지 고려하고 나머지 화살표 형태도 취합니다. x가 무한히 커지거나 작아질 때의 형태도 고려해야 합니다.$\lim_{\combi<x}\to\combi{\infty}}.{^{}\frac<x}{x^2+1}=0$limx→ ∞ xx2+1=0$\lim_{\combi<x}\to-\combi{\infty}}.{^{}\frac<x}{x^2+1}=0$limx→ − ∞ xx2+1=0

x가 무한대로 커지거나 작아지기 때문에 0으로 수렴하네요.위의 내용을 바탕으로 그림을 그려보세요.숫자 간격은 무시하고 마음대로 그렸어요. 그래프 모양만 보세요.아시겠어요?그림 하나로 최대값, 극소값 범위가 주어지면 최대값과 최소값도 쉽게 구할 수 있습니다.평면 운동에서의 속도직선운동에서의 속도는 이미 수학2로 배웠기 때문에 미적분 과목에서 새롭게 추가된 평면운동에서의 속도에 대해 정리해 보려고 합니다.문제를 같이 풀면서 볼게요.Q. 좌표평면 위를 움직이는 점 P의 시간 t에서의 위치(x, y)가 x=6t, y=6t-3t2일 때 점 P의 속도 최소값은?먼저속도좌표를잡아야겠죠?x와y를t로미분한(6,6-6t)이됩니다.속도는 속도의 크기이므로, $\sqrt{36+36t^2-72t+36}$√36+36t2-72t+36$=6\sqrt{\left(t-1\right)^2+1}$=6√(t-1)2+1이렇게 정리되시죠? 속도 최소치를 구하라고 하셨으니 답은 6이 되겠네요.기존 수학2의 도함수 활용으로 추가된 내용은 변곡점과 속도, 가속도 크기 정도인데 수식이 다소 복잡해지긴 하지만 (지수나 로그함수 미분, 몫 미분법 등 다양한 미분법이 등장했습니다) 기본 내용은 같아서 어렵게 느껴지지는 않을 것입니다.이제 미분은 다 끝나고 적분만 남았네요. 댓글에 오류가 있을 경우 댓글로 알려주세요.유리한 수정이었습니다.